世界を変えた17の方程式(前半)
世界を変えた17の方程式(前半)

■概要
数学者で一般向けのサイエンスライターであるイアン・スチュアート (Ian Stewart)が著書『世界を変えた17の方程式』で取り上げている17の方程式について解説する。
ここで扱うのは、その17の方程式に関する個人的な知識に基づく説明であり、著書の内容とは何ら関係ないことには注意してもらいたい。方程式にまつわる小話や歴史的背景なども挿入せず、単にその方程式が何を表すのかを説明するよう努める。またこの記事では、前半の1から9までだけを取り上げる。後半は『世界を変えた17の方程式(後半)』を参照。
■説明
1. ピタゴラスの定理(Pythagorean theorem)
$$a^2+b^2=c^2$$この定理は多くの人が馴染みあるものだろう。直角三角形の斜辺$c$の長さの二乗は、残りの二辺それぞれの長さの二乗の和であることを示す定理である。
2. 対数(Logarithms)
$$\log{xy}=\log{x}+\log{y}$$ $a$という数を二回かけ合わせたもの$a\times a$を$a^2$、三回かけ合わせたもの$a\times a\times a$を$a^3$と表す。これは、任意の自然$n$について同じで、$a$を$n$回かけ合わせたものは$a^n$と表される。では、$a$を何回かかけ合わせたら$x$になることがわかっていたとしよう。その何回かを$b$とすると、$a^b=x$である。これをひっくり返して、$b$に関する式として$$\log_a{x}=b$$と表す。これが$\log$という記号の意味であり、この「何回か」を表す$b$を対数という。
次に、$a$を$c$回かけたものが$y$、すなわち$a^c=y$だったとすると、$a^b$と$a^c$をかけあわせたものは、全部で$a$を$b+c$回かけあわせたものになるため、$a^b\times a^c=a^{b+c}$である。一方で、これらの積は$x\times y$でもあったから、これを対数の形にすると$$\log_a{xy}=b+c$$すなわち$$\log_a{xy}=\log_a{x}+\log_a{y}$$になる。このときの$a$を底というが、底がネイピア数$e$と呼ばれる特別な数であるとき、$$\log{x}=\log_e{x}$$などと省略して書かれることが多い。ただ、底が$10$の時も同じ略記がされることもあるので、$e$を底としていることを明示するために$\ln{x}$という表記がされることもある。
より詳しい解説は『指数・対数』の項を参照。
3. 微積分(Calculus)
$t$を変数とする関数$f(t)$の導関数$$\frac{df}{dt}=\lim_{h \rightarrow 0} \frac{f(t+h)-f(t)}{h}$$は、変数$t$がわずかに変化したときの$f(t)$の変化率を表している。導関数を得る操作を微分という。反対に、局所的な変化率から、変化分を積み上げて区間全体の変化を求める操作を積分と言う。
もっと詳しい説明は『微分とNewtonの運動方程式』および『積分と運動方程式の解』を参照してもらいたい。
4. ニュートンの重力の法則(Newton's law of universal gravitation)
$$F=G\frac{m_1 m_2}{r^2}$$は、それぞれ質量$m_1$と$m_2$を持つ物体同士が引き合う力の大きさを表している。互いの質量の比例しているので、重い物体ほど強い力を及ぼしあうことがわかる。また、物体間の距離$r$の二乗に反比例しているので、距離が離れれば離れるほど小さくなる。$G$は万有引力定数と呼ばれる定数である。 |
| 万有引力の法則:私たちは互いに惹かれあってる |
5. マイナス1の平方根(The square root of minus one)
$$i^2=-1$$は、二乗すると$-1$になる、という現実の物事に当てはめて考えることが困難な数、虚数(imaginary number)の定義である。より詳しい説明は『複素数の基礎』参照。
6. オイラーの多面体の公式(Euler's formula for polyhedra)
$$V-E+F=2$$は、任意の多面体において、頂点の数を$V$、辺の数を$E$、面の数を$F$とすると、この関係が成り立つということを主張するものである。例)正四面体であれば、$V=4$、$E=6$、$F=4$なので、$4-6+4=2$が確認できる。
7. 正規分布(Normal distribution)
$$\Phi(x)=\frac{1}{\sqrt{2 \pi \rho^2} } e^{\left(-\frac{(x-\mu)^{2}}{2 \rho^2}\right)}$$は、平均を$\mu$、分散を$\rho^2$とする確率分布である。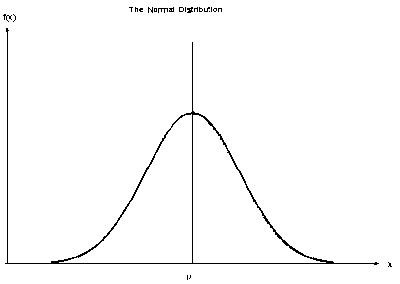
例えば物理的な例では、平衡状態にある気体の速度分布は正規分布の形をとる(マクスウェル-ボルツマン分布)。
8. 波動方程式(Wave equation)
$$\frac{\pd^2 u}{\pd t^2}=c^2 \frac{\pd^2 u}{\pd x^2}$$は、波の伝播を表している。$\pd/\pd t$というのは時間変化、$\pd/\pd x$は位置の変化、そして$c$は波の伝播速度を表している。$u$は波の高さと思えばいい。すなわち、波の時間変化率の時間変化率は、空間的な変化率の空間的な変化率に速度をかけたものに等しいということを表している。例えば、$u$を電場か磁場に変えると電磁波の方程式になり、$c$は光速を表すことになる。
9. フーリエ変換(Fourier transform)
なめらかで周期的な関数は、いろんな周波数($\omega$)の波(サイン関数やコサイン関数)の重ね合わせとして展開することができる。そして、その周期的な区間を無限に広げてやって、周期的でない関数も同じように(連続的な形で)展開できるようにしたのが、フーリエ変換$$f(\omega)=\int_{-\infty}^{\infty} f(x) e^{-2 \pi i x \omega} dx$$である。この式は、どんな周波数の波がどれくらい含まれているかを表している。言葉で説明するより、以下のアニメーションを見てもらった方が早いかもしれない。
このアニメーションでの$\hat{f}$が、上式の$f(\omega)$に対応している。【Fourier級数展開】 pic.twitter.com/wycdgWoYMk— 美しき物理学bot (@ST_phys_bot) June 17, 2019

後半はコチラ
世界を変えた17の方程式 [ イアン・スチュアート ]
posted with カエレバ





コメント